ロジ・ソリューションは、物流戦略の立案から物流実務のコンサルティングまで請け負っています。
様々なコンサルティングを行う際には、必ずと言って良いほど、配送実績、在庫実績等の現状の物流実態の把握を行います。また、物流現場改善を行う場合には、現場調査、アンケート調査を行い、調査結果を分析する必要があります。
色々なデータを使うことが日常的ですが、データを扱うには統計の知識が必要となってきます。
今回は、今後のデータ分析に活用できる、確率・統計の基礎を紹介したいと思います。
第1回目は、下記の第1章のデータの整理(記述統計学)を説明します。
第1章 データの整理(記述統計学)
- 統計学には、大きく「記述統計学」と「推測統計学」がある。
- 記述統計学:統計データの縮約を課題とする(始めにデータありき)。
- 分布・表・図:度数分布表、散布図、ローレンツ曲線、幹葉表示
- 特性値:平均、メディアン、標準偏差(分散)、相関係数
- 推測統計学:統計データを発生させた母集団の関して推論を行う。
- 統計データは、母集団から無作為標本抽出して得られた観測値たち(確率変数の実現値たち→標本データ)と捉える。
- 推論の基本パターン:推定(点推定、区間推定)、仮説検定
1.1はじめに
(1) 各記号の意味
統計を学ぶにあたって、計算式は必要不可欠である。計算式を使わない統計の書籍等があるが、実際に統計的分析をして顧客に説明をするには、その数字がどのように導き出されて、どのような意味を持つかを知っておく必要がある。
以降の説明では、計算式の記述があるが、はじめに計算式に出てくる記号の意味を説明したい。
1) 合計を表す
いま、「1,2,3,4,5」と言うデータがあるとする。この数字の和(足し算)をシグマ(Σ)記号を使って表してみると、![]() となる。この数式の意味は1+2+3+4+5のことである。
となる。この数式の意味は1+2+3+4+5のことである。
シグマ記号の下に書かれたi=1は、xと言うデータの集合(ここでは、1,2,3,4,5)の1番目、すなわち、1を意味している。シグマ記号の上に書かれた数値は、i=5までを変数xiに代入して合計することを意味する。
xiは、xと言うデータ集合のi番目のデータを表す。
上記の記載方法が正式であるが、ここでは、シグマ記号の上と下の表記を省略して表示している。
2) 平均を表す
平均を表す場合、一般的に「x̄」で表す。読み方は「エックスバー」と読む。
計算式は1.2 統計の基礎で説明する。
1.2 統計の基礎
(1) 平均:「データの和」を「データの数」で割ったもの。あるデータの集まりにおける中心の値を示す指標である。

(2) 偏差:平均からどのくらい離れているかを見る。データと平均との差。

(3) 偏差平方:偏差データを2乗したもの。偏差は個別のデータのバラツキを見ることができるが、データの集合としてバラツキを見る場合には適当ではない。2つのデータ群を比較する場合においては、両方とも偏差の合計値は「0」となってしまうためである。
例えば、データ群xi「5,6,7,8,9」とデータ群yi「3,5,7,9,11」の場合、xi、yiの平均は、両方とも「7」であり、それぞれのデータ群の偏差を見てみると下記のように「0」となる。

2つのデータ群のバラツキ度合いを比較する場合、偏差では不適当であり、偏差を2乗して合計したもの(偏差平方和)とすることで、比較が可能となる。

(4) 偏差平方和:偏差平方を合計したもの。

(5) 分散:データや分布のバラツキの程度を示す量。
偏差平方和は、データの数が多くなるほど値が大きくなる。膨大なデータを扱う際に、大きな値を見ても、感覚的にバラツキ度合いを比較するのは困難である。そこで、偏差平方和をデータの数で割って、バラツキの尺度とする。これを分散と言う。

(6) 標準偏差:分散の平方根をとって、データの平均と同じ単位にしたもの。
分散でバラツキ度合いを見たが、分散はデータを2乗したものであり、元々のデータとは単位が異なる。つまり、単純に元データと分散を比較することはできない。そこで、元データの単位と揃えるために、分散の「平方根」をとることにする。

(7) 変動係数:相対的なバラツキの指標。標準偏差を平均で除したもの。データの単位が異なる項目について、バラツキの比較が可能となる。

(8) 標準化データ:データを、平均=0、標準偏差(分散)=1のデータに直したもの。偏差を標準偏差で除すことで求められる。

(9) 偏差値:標準化データを10倍して50を加算したもの。学校の試験等で利用される。

(10) メディアン:データを大きさの順に並べた時の真ん中の値。中央値とも言う。
(11) モード:最も度々現れる値のこと。最頻値とも言う。
1.3 度数分布とヒストグラム
(1) 階級:観測値のとりうる値の範囲
(2) 度数:階級に含まれるデータの個数
(3) 相対度数:測定値の総数(全データ数)の大きさを 1 とした時の、各階級に属する測定値の個数の総数に対する割合
(4) 累積度数:度数を下の階級から順に加算した時の度数
(5) ヒストグラム:度数分布表から得られる柱状グラフ
*例.試験得点の度数分布表

*例.試験得点のヒストグラム

1.4 二変数データ(散布図と相関係数)
ここでは、二つの変数xとyを対で観測して得られた、サイズnのデータを考察対象とする。
(1) 散布図:二つの要因の因果関係を見たい時に使用する(量的データでサイズnがあまり大きくない場合)。
(2) 相関係数:ある量とある量との線形な関係度を表わす指標で-1と1の間の値をとる。1に近い時は強い相関があると言い、-1に近い時は負の強い相関があると言う。
0の場合は、2変数に相関関係はなく、無相関となる。


(3) 相関係数の値の大雑把な目安
1) 0.0~0.2 (-0.2~0.0) :ほとんど相関なし
2) 0.2~0.4 (-0.4~-0.2) :やや[正の(負の)相関あり]
3) 0.4~0.7 (-0.7~-0.4) :かなり[正の(負の)相関あり]
4) 0.7~1.0 (-1.0~-0.7) :かなり強い[正の(負の)相関あり]
(4) 偏差積和:散布図上の点が直線状になっている程度を数量的に表したもの。

(5) 共分散:偏差積和をデータの個数で割ったもの。偏差積和では、データの値が大きいと、その絶対値が大きくなる傾向があるため、データの個数で割っている。

(6) 偏差積和Sxy(共分散Sxy)の意味合い-サイズnの2次元データを次のように4分割する。
1) 二変数x,yについて、ともに平均以上の観測値をⅠ象限
2) 変数xは平均未満、一方、変数yは平均以上の観測値をⅡ象限
3) 二変数x,yについて、ともに平均未満の観測値をⅢ象限
4) 変数xは平均以上、一方、変数yは平均未満の観測値をⅣ象限
この時、偏差積和は、Ⅰ象限≧0、Ⅱ象限≦0、Ⅲ象限>0、Ⅳ象限<0となる。

2.1 実際のデータによる統計的手法の利用法
【課題】鉱工業生産指数とトラックの輸送物量(トン)の関係を分析する。
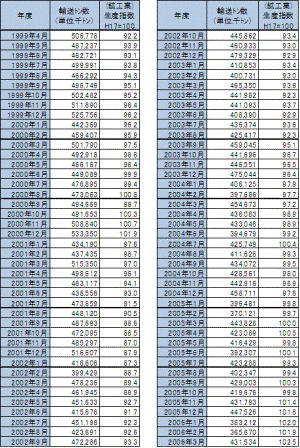
1.対象データ
(1) トラックの輸送物量:陸運統計要覧-自動車貨物輸送量の推移
* 自家用・営業用の合計値を使用。
(2) 鉱工業生産指数:内閣府ホームページ
2.対象期間
・1999年4月~2006年3月(両データの重複期間)
Ⅱ.分析内容
1. 基本分析
(1) 平均
1) 輸送トン数
・平均=(506,778+487,237+…+431,534)÷84(データの数)=450,362
2) 鉱工業生産指数
・平均=(92.2+93.9+…+102.5)÷84(データの数)=96.5
(2) 分散
1) 輸送トン数
・分散
={(506,778-450,362)^2+(487,237-450,362) ^2+…+(431,534-450,362) ^2}÷84=1,367,912,994
2) 鉱工業生産指数
・分散={(92.2-96.5)^2+(93.9-96.5)^2+…+(102.5-96.5)^2}÷84=15.7
(3) 標準偏差
1) 輸送トン数
・標準偏差=√1,367,912,994=37,107
2) 鉱工業生産指数
・標準偏差=√15.7=3.96
(4) 変動係数
1) 輸送トン数
・変動係数=標準偏差÷平均=37,107÷450,362=0.082
2) 鉱工業生産指数
・変動係数=標準偏差÷平均=3.96÷96.5=0.041
(5) メジアン
1) 輸送トン数
・メジアン=447,039
2) 鉱工業生産指数
・メジアン=96.5
(6) モード
1) 輸送トン数
・モード=なし
2) 鉱工業生産指数
・モード=93.0
(7) 度数分布表
1) 輸送トン数
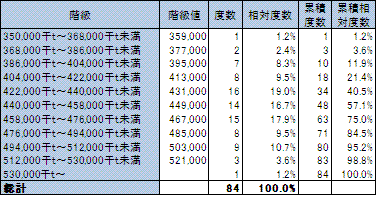
2) 鉱工業生産指数
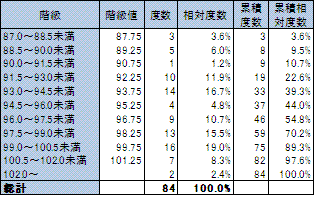
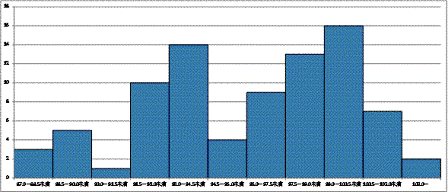
(8) ヒストグラム
1) 輸送トン数
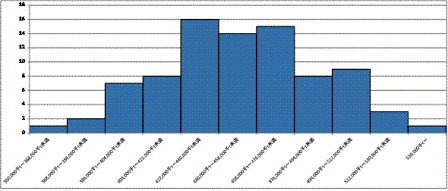
2) 鉱工業生産指数
(9) 散布図
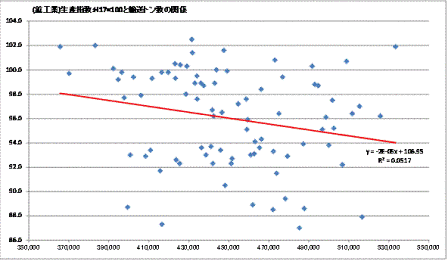
(10) 相関係数
・相関係数=共分散÷(輸送トン数の標準偏差×鉱工業生産指数の標準偏差)
={(506,778-450,362)×(92.2-96.5)+(487,237-450,362)×(93.9-96.5) +…+(431,534-450,362)×(102.5-96.5)÷84}÷(37,107×3.96)= -0.2275
(7)~(10)の数値をはっきり確認したい場合はこちら
Ⅲ.結論
1.変動係数は、輸送トン数0.082に対して、鉱工業生産指数0.041であり、輸送トン数の方が相対的なバラツキが大きい。
2.輸送トン数と鉱工業生産指数の相関係数は-0.02275であり、やや負の相関がみられる。
つまり、鉱工業生産指数が上昇すれば、トラックの輸送割合は減少する。
3.今回の分析は、統計を実際に使ってみることに重点を置いており、実際にトラック輸送量の増減を分析する場合には、鉱工業以外の業種の動向、他の輸送手段の増減、燃料価格等も合わせて分析する必要があることを注意したい。
Ⅴ.まとめ
・今回の分析は、マイクロソフト社のエクセルを利用すれば簡単に計算できるものである。しかし、統計とはどういったもので、その数値が何を意味するかを知ることが重要である。「機械が算出した結果なので良く分からない」では、コンサルタントとして顧客に説明はできない。データを扱う仕事をする人にとっては、統計は知っていて損はない。これを機会に、統計を学んでみることを勧める。
【参考】
・東京大学教養学部統計学教室編 「統計学入門」 東京大学出版会
・長谷川勝也 「確率・統計のしくみがわかる本」 株式会社技術評論社
・石村貞夫、デズモンド・アレン 「すぐわかる統計用語」 東京図書株式会社
・中村・新家・美添・豊田 「統計入門」 東京大学出版会
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
★掲載された記事の内容を許可なく転載することはご遠慮ください。
ロジ・ソリューションでは、物流に関するいろいろなご支援をさせていただいております。
何かお困りのことがありましたらぜひお声掛けください。